Where mathematics and a social perspective meet data

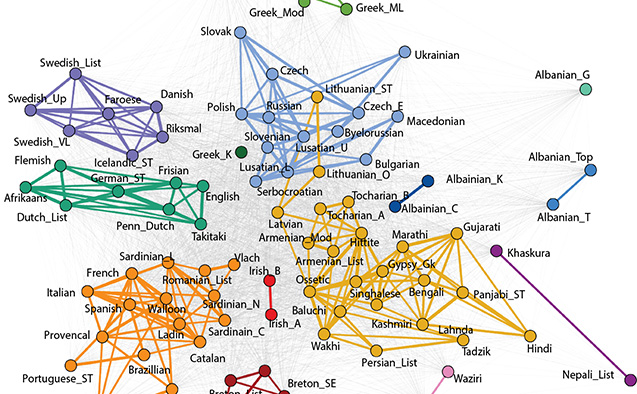
Community structure, including relationships between and within groups, is foundational to our understanding of the world around us. New research by mathematics and statistics professor Kenneth Berenhaut, along with former postdoctoral fellow Katherine Moore and graduate student Ryan Melvin, sheds new light on some fundamental statistical questions.  

 “When we encounter complex data in areas such as public health, economics or elsewhere, it can be valuable to address questions regarding the presence of discernable groups, and the inherent “cohesion” or glue that holds these groups together. In considering such concepts, socially, the terms “communities,” “networks” and “relationships” may come to mind,” said Berenhaut.

The research leverages abstracted social ideas of conflict, alignment, prominence and support, to tap into the mathematical interplay between distance and cohesiveness – the sort evident when, say, comparing urban and rural settings. This enables adaptations to varied local perspectives.

“For example, we considered psychological survey-based data reflecting differences and similarities in cultural values between regions around the world – in the U.S., China, India and the EU,” Berenhaut said. “We observed distinct cultural groups, with rich internal network structure, despite the analytical challenges caused by the fact that some cohesive groups (such as India and the EU) are far more culturally diverse than others. Mark Twain once referred to India as ‘the country of a hundred nations and a hundred tongues, of a thousand religions and two million gods.’ Regions (such as the Southeast and California in the U.S.) can be perceived as locally distinct, despite their relative similarity in a global context. It is these sorts of characteristics that we are attempting to detect and understand.”

The paper, “A social perspective on perceived distances reveals deep community structure,” published by PNAS (Proceedings of the National Academy of Sciences of the United States) can be found here.

“I am excited by the manner in which a social perspective, along with a probabilistic approach, can illuminate aspects of communities inherent in data from a variety of fields,” said Berenhaut. “The concept of data communities proposed in the paper is derived from and aligns with a shared human social perspective. The work crosses areas with connections to ideas in sociology, psychology, mathematics, physics, statistics and elsewhere.”

Leveraging our experiences and perspectives can lead to valuable mathematical and statistical insights.